A
golygon (technically referred to as a "serial isogon of 90 degrees") is any
polygon with all
right angles, whose sides are consecutive integer lengths. Golygons were invented and named by
Lee Sallows, and popularized by
A.K. Dewdney in a 1990
Scientific American
column (Smith). Variations on the definition of golygons involve
allowing edges to cross, using sequences of edge lengths other than the
consecutive integers, and considering turn angles other than 90°.
In any golygon, all horizontal edges have the same
parity as each other, as do all vertical edges. Therefore, the number
n of sides must allow the solution of the system of equations

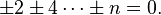
It follows from this that
n must be a multiple of 8.
The number of solutions to this system of equations may be computed efficiently using generating functions (sequence
A007219 in
OEIS) but finding the number of solutions that correspond to non-crossing golygons seems to be significantly more difficult.



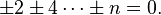



No comments:
Post a Comment